Полет

Движение тела фигуриста в полете при выполнении многооборотного прыжка может быть рассмотрено как движение тела вместо с, осью вращения и вокруг этой оси. На рис. 15 приведены три последовательных положения тела в начале, в середине и в конце полета. Мывидим, что в каждый момент полета тело фигуриста участвует в двух указанных движениях.

Анализ кинограмм показал, что в хорошо выполненном прыжке движение оси вращения тела близко к поступательному. В результате сложное движение тела в полете можно рассматривать как движение поступательное вместе с осью вращения и вращательное вокруг оси вращения. Известно, что при поступательном движении все точки тела в определенный момент имеют одинаковые векторы скоростей и ускорений. Следовательно, исследование движения оси вращения его можно заменить исследованием движения точки. В качестве такой точки удобно выбрать о. ц. т., через который на протяжении всего безопорного периода проходит ось вращения.

Рис. 15. Сложное движение тела в полете: V1, V2, V3 - скорости движения о. ц. т. тела; ω1, ω2 ω3 - угловые скорости вращения тела

Следует отметить, что разложение сложного движения на поступательное и вращательное является исследовательским приемом, в то время как в действительности оба движения тесно взаимосвязаны и являются двумя сторонами единого движения.

Уравнение движения центра тяжести тела, брошенного под углом к горизонту, в проекциях на оси координат χ и у без учета сопротивления воздушной среды выглядит следующим образом:

где а_о — угол вылета; К_о — начальная скорость вылета; Ј —ускорение свободного падения.

Уравнение показывает, что форма траектории, а следовательно, и максимальная высота и дальность прыжка зависят лишь от начальных параметров движения о. ц. т.: начальной скорости вылета (Vo) и угла вылета (ао) при постоянном ускорении свободного падения (g).

Таким образом, траектория движения о. ц. т. тела в безопорном периоде определяется лишь углом вылета и начальной скоростью полета (по форме это парабола - рис. 16). Никакими вращениями конечностей, перемещениями и т. п. изменить ее в полете нельзя.

Рис. 16. Траектория о. ц. т. тела в полете: Vo — начальная скорость вылета; Vверт - составляющие скорости движения о. ц. т. тела; l — длина полета о. ц. т.; hmax— максимальная высота подъема о. ц. т. тела

Отсюда вытекает важный практический вывод: характер движения о. ц. т. тела в безопорпом периоде целиком определяется толчком. Параметры движения о. ц. т. тела фигуриста в полете мы определяли методом кишщиклографии (табл. 2). У мастеров спорта, отличающихся высоким мастерством исполнения прыжков, были измерены параметры движения о. ц. т. в полете в прыжках двойной лутц и двойной аксель. Оказалось, что у каждого исполнителя начальная скорость вылета в этих прыжках приблизительно одинакова, угол вылета различный: в прыжке аксель он больше (32—34°), в прыжке лутц — меньше (21—28°). Различие угла вылета можно объяснить тем, что в прыжке аксель стопорящее движение, как правило, выражено более сильно. Большая величина угла вылета в прыжке двойной аксель дает большую высоту подъема о. ц. т. тела.

Таблица 2

Параметры движения о. ц. т. тела в полете

Характер вращательного движения тела в полете существенно влияет на качество выполнения прыжка. И недостаточный, и чрезмерный поворот тела в полете затрудняет выполнение приземления. Пренебрегая сопротивлением воздушной среды, можно считать, что в полете на тело фигуриста действует лишь внешняя сила — сила веса. Момент этой силы относительно о. ц. т. тела равен нулю, поэтому, чтобы проанализировать вращательное движение, можно воспользоваться законом сохранения момента количества движения, согласно которому количество вращательного движения, приобретенное фигуристом в толчке, постоянно на протяжении всего полета, т. е. K = J ·ω = const, где К — момент количества движения (запас вращательного движения); J — момент инерции тела, характеризующий степень группировки фигуриста; ω— угловая скорость вращения.

Этот закон является основным при анализе вращательного движения тела в безопорном периоде. Фигурист в полете выполняет группировку и разгруппировку, т. е. определенным образом перемещает звенья тела относительно оси вращения, чем изменяет момент инерции тела. Приближенно минимальный момент инерции тела относительно продольной оси у фигуриста ростом 170 см и весом 60 кг равен 0,12 кГм.сек². С помощью зенитной съемки со скоростью 100 кадров в секунду с применением электронного отметчика времени мы определяли значение угловой скорости вращения в полете в момент наиболее плотной группировки. Исходя из этих данных, можно приближенно определить величину момента количества движения, которым обладает тело фигуриста в полете.

На рис. 17 изображен график изменения угловой скорости в прыжке в 2,5 оборота. Точки 1, 2, 3 соответствуют группировке, точка 4 — фиксации группировки, точки 5, 6, 7 и 8 — разгруппировке. Момент количества движения, которым обладало тело фигуриста в полете, приблизительно равен 3 кГм.сек.

При рассмотрении вращательного движения в полете очень важно определить влияние величины момента количества движения на параметры вращательного движения. На рис. 18 изображены графики зависимости угловой скорости вращения тела в полете для трех различных значений момента количества движения: Κ\==ί кГм.сек, Й*2 = 3 кГм.сек, Кг = 5 кГм.сек. Выделим область возможного изменения момента инерции тела фигуриста в прыжке. Сравним, при каком значении момента количества движения достигается наибольшая скорость вращения. Мы видим, чем больше величина момента количества движения, которым обладает тело, или, другими словами, чем большее вращательное движение приобретено фигуристом в толчке, тем при прочих равных условиях больше угловая скорость вращения.

Скорость вращения тела фигуриста в прыжках определяется начальными условиями, т. е. моментом количества движения, приобретенным в толчке, и движениями в полете — группировкой и раз-группировкой. Обращает на себя внимание тот факт, что часть номинального, т. е. опредедяемого названием прыжка, поворота фигурист выполняет в конце толчка и в начале приземления.

При этом поворот тела вокруг продольной оси представляет собой единое движение, сопровождающееся группировкой, фиксацией группировки и разгруппировкой, и выполняется в опорных и безопорной фазах прыжка.

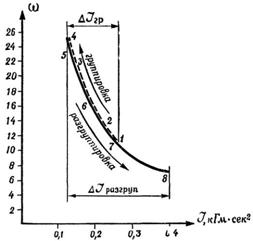Рис. 17. График изменения скоро-сти вращения тела в полете в зави-симости от плотности группировки в прыжке двойной аксель: ω — угловая скорость вращения тела в полете; / — момент инерции тела относительно продольной оси; Δ/ — изменение момента инерции в результате группировки; Δ/ разгруп~ изменение момента инерции в результате разгруппировки

Рис. 18. Графики угловой скорости вращения тела в полете для трех значений момента количества движения: ffi, Η2, К3 — различные величины момента количества дви-жения; Δ/Β03Μ.— возможное изменение момента инерции тела при группировке

Измерения скорости вращения тела показывают, что характер изменения угловой скорости в прыжках различный. Объясняется это тем, что начало группировки, ее скорость и плотность, длительность фиксации, скорость разгруппировки зависят от числа оборотов прыжка, стиля и манеры исполнения. Однако среди большого разнообразия кривых угловой скорости вращения тела можно выделить две группы, соответствующие двум основным способам выполнения прыжков: с фиксацией группировки и без фиксации ее.

В прыжках с максимальным для спортсмена числом оборотов фиксация группировки, как правило, есть. Таким способом выполняют, в основном, прыжки в два и более оборотов. Прыжки одинарные и так называемые «раскрытые» прыжки выполняют без фиксации группировки. На рис. 19 приведены схемы изменения угловой скорости вращения тела в прыжках аксель, двойной аксель и тройной лутц. Группировка в прыжке аксель - без выраженной фиксации (рис. 19, а). В отличие от одинарного акселя, в прыжках с большим числом оборотов кривые изменения скорости имеют более выраженный участок фиксации скорости вращения (рис. 19, б, в).

Рис. 19. Схемы изменения угловой скорости вращения тела в различных прыжках: а - аксель; б - двойной аксель; в - тройной лутц

Существуют различные варианты выполнения прыжков (в зависимости от способа группировки). Прыжок аксель в 1,5 оборота и некоторые двойные прыжки часто выполняют в затяжном и открытом вариантах. В затяжном варианте прыжка фигурист отрывается от поверхности льда в возможно более разгруппированном положении и группируется, только пройдя верхнюю точку траектории. Со стороны кажется, что он повисает в воздухе. Мнение о том, что благодаря наибольшему изменению момента инерции этот вариант группировки обеспечивает максимальную угловую скорость, ошибочно. При постоянном значении момента количества движения максимальная угловая скорость зависит только от минимального значения момента инерции, определенного положением наиболее плотной группировки.

Рис. 20. Варианты выполнения группировки в прыжках: Jmin, Jcp,, Jmax—минимальное, среднее и максимальное значения момента инерции тела фигуриста относительно продольной оси: а, в, с — точки, соответствующие минимальному, среднему и максимальному значениям момента инерции тела

Для открытого варианта выполнения прыжков характерно разгруппированное положение тела на протяжении всего полета. Отсутствие выраженной группировки делает открытые прыжки очень эффектными. Однако из-за низкой средней угловой скорости этот вариант группировки неприемлем для прыжков с максимальным числом оборотов.

Описанные варианты выполнения группировки в прыжках могут быть выражены графически. На рис. 20 отмечена область возможного изменения момента инерции тела фигуриста. Участок а—с соответствует группировке в затяжных прыжках, в—с — группировке в открытых прыжках, а—в — группировке в прыжках с максимальным числом оборотов.