 Взаимное положение звеньев тела фигуриста при выполнении обязательных фигур бесконечно разнообразно. Однако все это многообразие может быть систематизировано по отдельным признакам*. Взаимное положение звеньев тела фигуриста при выполнении обязательных фигур бесконечно разнообразно. Однако все это многообразие может быть систематизировано по отдельным признакам*.
Наибольшее распространение получила система положений, обоснованная Н. А. Паниным в 1928 г. и опубликованная в 1933 г. в третьем издании книги «Фигурное катание на коньках».
Признак, который Н.А.Панин положил в основу своей систематизации,—это взаимное расположение фронтальных (поперечных) осей плечевого пояса и таза. Согласно этому признаку, могут существовать две группы положений: в одной ось плечевого пояса и ось таза лежат приблизительно в одной вертикальной плоскости (рис. 1 а), в другой они скрещиваются, т е. повернуты от среднего положения в противоположные стороны (рис. 1 б). Эти положения рассматриваются отвлеченно—в пространстве без опоры.
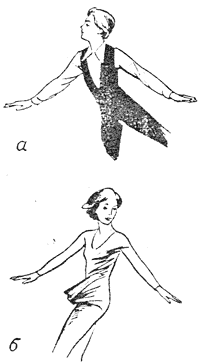 |
| Рис. 1. Положения тела фигуриста: а — нескрученнос; б - скрученное |
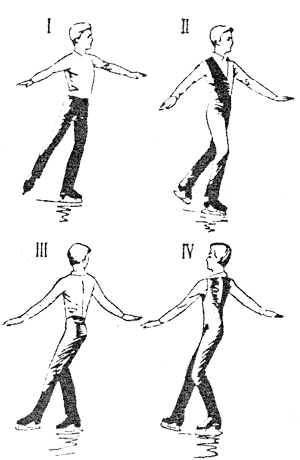 |
| Рис. 2. Четыре позиции фигуриста |
При рассмотрении положений тела фигуриста в условиях опоры возникает необходимость различать опорную и свободную ноги. Признак взаимного расположения фронтальных осей плечевого пояса и таза дополняется признаком расположения свободной ноги относительно опорной. С учетом этого признака положения тела при выполнении обязательных фигур могут быть приближенно сведены к четырем (рис. 2):
I позиция — плечевой пояс и таз повернуты относительно среднего положения в одну сторону, свободная нога сзади опорной;
II позиция — плечевой пояс и таз повернуты относительно среднего положения в противоположные стороны, свободная нога сзади;
III позиция — плечевой пояс и таз повернуты относительно среднего положения в одну сторону, свободная нога впереди опорной;
IV позиция — плечевой пояс и таз повернуты относительно среднего положения в противоположные стороны, свободная нога впереди опорной.
Приведенные позиции существуют независимо от ребра и фронта скольжения.
Для более четкого описания положения свободной ноги. относительно опорной будем пользоваться выражениями «впереди» и «сзади», а также «сомкнута» и «разомкнута». Например, свободная нога впереди сомкнута или свободная нога сзади разомкнута.
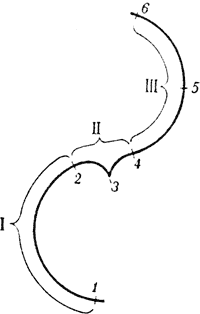
При описании поворотов принята следующая схема разделения движений на периоды и фазы (рис. 3):
1-2 - период подготовки к повороту;
2—4 — период разрешения поворота (2—3 — фаза въезда, 3—4 — фаза выезда);
4—6— период завершения поворота (4—5 — фаза фиксации позы, 5-6 - фаза перемены позиции).
К основным движениям относятся скольжение, вращательные движения звеньев тела и отталкивание.
Скольжение
Движения тела фигуриста при скольжении по дуге характеризуются такими величинами, как скорость, ускорение, ра-
диус кривизны дуги скольжения, сила инерции, давления конька на лед, сила трения. Для того чтобы определить, как они связаны, рассмотрим схему одноопорного скольжения (рис. 4).
 |
| Рис. 3. Разделение движений в повороте на периоды и фазы |
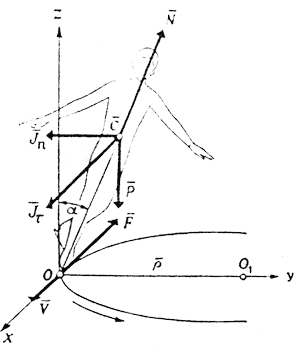 |
| Рис. 4. Силы, действующие на фигуриста при одноопорном скольжении |
<рp>На тело фигуриста, скользящего по дуге окружности радиуса  , имеющего в данный момент скорость v, действуют: сила веса Р, сила трения F, направленная в сторону, противоположную движению; касательная сила инерции , имеющего в данный момент скорость v, действуют: сила веса Р, сила трения F, направленная в сторону, противоположную движению; касательная сила инерции 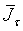 , параллельная оси Ох и направленная противоположно замедлению; нормальная (центробежная) сила инерции , параллельная оси Ох и направленная противоположно замедлению; нормальная (центробежная) сила инерции  , параллельная оси Оу; опорная реакция N, равная давлению фигуриста на лед и направленная по продольной оси вверх. , параллельная оси Оу; опорная реакция N, равная давлению фигуриста на лед и направленная по продольной оси вверх.
В рассматриваемый момент тело фигуриста находится в координатной плоскости zOy, продольная ось наклонена на угол  к вертикали; l-расстояние от о. ц. т. тела до точки опоры 0. к вертикали; l-расстояние от о. ц. т. тела до точки опоры 0.
Составим уравнения равновесия сил и моментов, для чего спроектируем все силы на координатные оси, а также составим уравнения моментов этих сил относительно осей координат:

Наибольший интерес представляют четыре первых уравнения. Подставляя вместо сил инерции и силы трения их выражения, получим*:
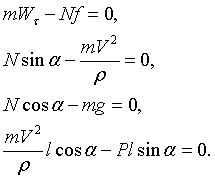
Рассмотрим ряд практических выводов, которые можно сделать, анализируя приведенные уравнения.
Важной характеристикой скольжения является наклон продольной оси тела к поверхности льда. Он тесно связан с peберностью скольжения, а реберностъ скольжения —одно из, основных условий высокого качества выполнения фигуры.
Преобразуя уравнение (4), получаем:

где  — радиус кривизны следа. — радиус кривизны следа.
В формулу не входит масса тела. Отсюда первый важный вывод: угол наклона продольной оси тела фигуриста зависит только от величины радиуса дуги и скорости скольжения; он не зависит от массы, а следовательно, и от веса фигуриста.
Из формулы (5) можно сделать другой вывод: угол наклона продольной оси увеличивается пропорционально квадрату скорости скольжения; он уменьшается с увеличением радиуса дуги скольжения.
Подсчитаем угол отклонения продольной оси тела от вертикали для фигуриста, который после отталкивания начал скользить по дуге окружности радиусом 3 м, имея скорость 2,4 м/с:

откуда 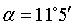 . .
При скольжении с меньшей скоростью угол наклона меньше. Известно, что при малых углах наклона опорная нога может оставить на льду двуреберный след, а это грубая ошибка.
Формула (5) связывает между собой четыре величины. Следовательно, каждую из величин можно выразить через остальные. Например, скорость скольжения будет равна;
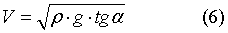
Из той же формулы (5) можно определить выражение для радиуса кривизны дуги скольжения:
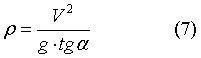
При изучении техники обязательных фигур важно знать силы взаимодействия конька со льдом.
Равенство (3) позволяет определить величину давления конька опорной ноги на лед:

Так как косинус угла всегда меньше единицы, то из формулы (8) следует важный вывод: при скольжении по дуге давление конька на лед всегда больше веса фигуриста и равно ему при скольжении по прямой.
Для более детального анализа зависимости величины давления конька на лед воспользуемся уравнением (2):
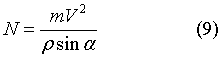
Как видим, давление на лед зависит от массы тела фитуриста, квадрата скорости, радиуса кривизны дуги скольжения и синуса угла наклона продольной оси тела фигуриста. Давление возрастает с увеличением массы тела фигуриста и скорости его скольжения и убывает с увеличением радиуса кривизны дуги и угла наклона продольной оси тела. При a =90°, т. е. когда ось расположена горизонтально, sin a = 1, формула (9) принимает вид:
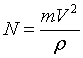
Иными словами, мы получим выражение, из которого видно, что причиной увеличения давления конька на лед является нормальная (центробежная) сила инерции, появляющаяся при скольжении по кривой.
Одной из проблем выполнения обязательных фигур, особенно в форме восьмерки, является сохранение такой величины скорости скольжения, которая обеспечивает реберность скольжения и высокое качество поворотов на протяжении всей фигуры.
Рассмотрим причины, вызывающие Замедление скольжения. Условимся, что в это время фигурист не выполняет поворотов и перетяжек, а также не сгибает и не разгибает опорную ногу.
Основной тормозящей силой при скольжении в обязательных фигурах является сила трения (сопротивление воздуха при малых скоростях незначительно). Определим связь величины замедления с коэффициентом трения конька о лед. Из равенства (1) можно определить замедление при одноопорном скольжении:

Как видим, при одноопорном скольжении замедление прямо пропорционально давлению на лед, коэффициенту трения и обратно пропорционально массе тела.
Для определения численного значения замедления в ряде случаев удобно воспользоваться другим видом формулы (10) После преобразования ее мы получаем:
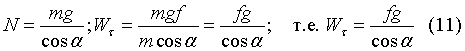
Из формулы (11) видно, что при одноопорном скольжении замедление прямо пропорционально коэффициенту трения конька о лед и обратно пропорционально косинусу угла наклона продольной оси тела фигуриста.
Поскольку на практике величина cos а меняется незначительно, а ускорение силы тяжести g— величина постоянная для данного места, то замедление зависит главным образом от коэффициента трения конька опорной ноги о лед. Коэффициент трения скольжения зависит от многих причин: от качества льда, его температуры и состава воды, от материала, из которого сделано лезвие конька, и его заточки. Чем ниже температура льда, тем больше коэффициент трения. На качество льда влияет количество минеральных солей, растворенных в воде. Лед, полученный из жесткой воды, создает большее сопротивление скольжению, чем лед из мягкой воды. При низкой температуре лед тверже, а при повышенной мягче. В первом случае скольжение затрудняется из-за твердости льда, а во втором из-за того, что лезвие конька врезается в мягкий лед.
Коэффициент трения на хорошем льду минимален, что уменьшает величину замедления при скольжении. Величина коэффициента трения стали о лед колеблется в пределах 0,01-0,03.
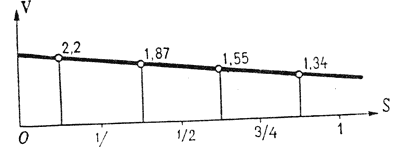
Подсчеты показывают, что при выполнении круга вперед-наружу средние величины скорости на каждой четверти окружности равняются:
V1 = 2,2 м/с, V2 = 1,87 м/с, V3 = 1,55 м/с, V4 = 1,34 м/с. На рис. 5 приведен график уменьшения скорости скольжения при выполнении круга вперед-наружу. Как видим, характер уменьшения скорости соответствует равнозамедленному движению. Другими словами, у квалифицированных фигуристов замедление при простом скольжении по дугам практически постоянно.
При выполнении сложных фигур (простая восьмерка со скобками, восьмерка с двукратными тройками и особенно восьмерки назад с тройкой) характер падения величины скорости скольжения нелинейный. В первой половине фигуры уменьшение скорости скольжения незначительно, однако во второй ее половине начинает проявляться следующая зависимость. Уменьшение скорости скольжения вызывает уменьшение угла-наклона конька ко льду, переход к скольжению на плоскости конька и как следствие увеличение площади опоры и увеличение сил трения. В результате при выполнении сложных фигур скольжение фигуриста не равнозамедленно, и скорость убывает нелинейно. Чем ниже квалификация спортсмена, тем ярче выражена нелинейность тем сильнее замедление в конце фигуры.
У фигуристов высокого класса благодаря качественному реберному скольжению, отсутствию скобления льда в поворотах и умению набирать ход при их выполнении падение скорости от начала фигуры к концу выражено слабее.
Повороты
При выполнении обязательных фигур тело участвует во вращательных движениях. В специальной литературе сложное движение тела фигуриста при скольжении по дуге принято делить на поступательное и вращательное. При таком разделении выпадала из виду одна из важных особенностей движения, имеющая принципиальное значение для изучения техники поворотов в обязательных фигурах. Рассмотрим схему движения фигуриста при скольжении по дуге окружности.
На рис. 6 приведено схематическое изображение (вид сверху) такого скольжения. Отчетливо видно, что во время скольжения по окружности тело фигуриста вращается вокруг оси, проходящей через центр окружности. При выполнении одного круга опорная нога и ее конек совершают одйн оборот т. е. поворот на 360°. Другими словами, тело участвует во вращательном движении, а не в поступательном. Видно также, что точки тела, расположенные на разном расстоянии от центра окружности, имеют разные величины скоростей движения. Это еще раз подчеркивает, что нельзя говорить о поступательном движении тела фигуриста при скольжении по дуге: известно, что при поступательном движении скорости всех точек тела в данный момент одинаковы.
 |
| Рис. 5. Уменьшение скорости скольжения при выполнении круга вперед-наружу |
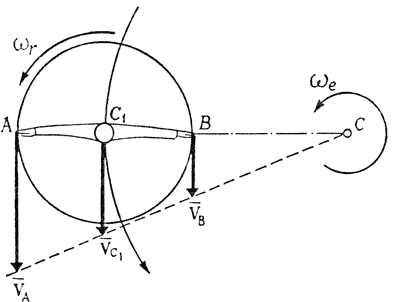 |
| Рис. 6. Схема движения тела фигуриста при скольжении по окружности |
Итак, скольжение фигуриста по окружности есть движение вращательное.
Значительную часть элементов обязательных фигур составляют повороты. Замечено, что в основе выполнения поворотов лежат вращательные движения. Здесь очень важно правильно понимать причины, вызывающие поворот. В литературе имеются утверждения, что механизм вращательных компонентов поворота заключается в изменении угловой скорости вращения тела изменением момента инерции путем приближения или удаления звеньев тела от оси вращения.
Рассмотрим, можно ли выполнить поворот, приближая к продольной оси и удаляя от нее звенья тела, т. е. с помощью изменения момента инерции тела относительно , продольной оси. Напомним: если тело в целом не имеет начального вращения вокруг своей продольной оси, то в отсутствие внешних сил ни приближения, ни удаления звеньев не могут вызвать вращения.
Итак, можно ли выполнить поворот с помощью приближения и удаления звеньев тела.
Случай I. Фигурист, пытаясь сделать поворот одним из способов (при толчке или скольжении по дуге), сообщает телу вращение в положительном направлении. Тело начинает вращаться вокруг оси мгновенного вращения, расположенной внутри окружности. Кривая скольжения будет закругляться. В момент группировки рук и свободной ноги резко увеличивается скорость вращения тела в положительном направлении. Плечевой пояс, таз, опорная нога, ее конек начинают поворачиваться. Для замедления вращения фигурист разгруппировывается, скорость вращения тела падает, в результате дальнейшее скольжение конька происходит по более пологой дуге. Однако тело продолжает вращаться в направлении, которое получено при толчке.
Приведенная схема движения приближенно соответствует схеме выполнения тройки и показывает принципиальную возможность сделать ее, изменяя момент инерции тела фитуриста относительно продольной оси.
Другой поворот, подготовка к которому осуществляется в положительном направлении,—крюк. Приближение и удаление звеньев тела могут изменить лишь величину скорости вращения тела, но не его направление. В крюках направление скольжения конька до и после поворота противоположно
Сказанное может быть подтверждено практическими попытками выполнить таким способом крюк на льду. Сообщив своему телу общее вращение в положительном направлении, фигурист, приближая руки к продольной оси тела и стремясь выполнить крюк, будет выполнять поворот тройкой.
Случай 2. Фигурист, скользя по дуге, вращением верхней части тела сообщил всему телу вращение в отрицательном направлении. В результате сложения двух вращений, направленных в разные стороны (вокруг центра фигуры и вокруг своей продольной оси), ось мгновенного вращения тела смещается наружу круга, дуга постепенно уплощается. Группируя руки и свободную ногу, фигурист увеличивает скорость, вращения тела в отрицательном направлении. Плечевой пояс, туловище, таз увлекают во вращение опорную ногу, возникает поворот в сторону общего вращения тела. Затем выполняется разгруппировка и как следствие переход к скольжению по более пологой дуге.
При этом, естественно, сохраняется общее вращение тела в направлении поворота, а скольжение происходит в направлении, совпадающем с направлением вращения тела, полученного до поворота. Такая схема поворота соответствует выкрюку и, подобно повороту тройкой, показывает принципиальную возможность выполнения поворота выкрюком с помощью приближения звеньев тела к оси вращения.
Описанная схема движения показывает также, что поворот скобкой не может быть выполнен этим способом, так как здесь направление скольжения при завершении элемента должно быть противоположно направлению общего вращения тела, полученного перед поворотом. А, как мы уже говорили, изменение момента инерции тела не может изменить направление его поворота. Принципиальную невозможность выполнить поворот скобкой приближением звеньев тела к продольной оси тела и удалением от нее можно убедительно доказать также на практике.
Таким образом, утверждения о том, что механизм вращательного компонента поворота заключается в изменении угловой- скорости вращения тела с помощью изменения момента инерции для скобок и крюков, принципиально неверны. Другими словами, ни скобку, ни крюк невозможно выполнить приближая руки и свободную ногу к продольной оси тела или удаляя от нее.
Мы уже говорили, что существует принципиальная возможность выполнить повороты тройкой и выкрюком с помощью группировки рук и свободной ноги, предварительно сообщив телу начальное вращение. Реальная попытка нарисовать на льду фигуру с тройками, например любую фигуру в форме восьмерки или крюк, используя этот способ выполнения поворотов, окажется безрезультатной. Дело в том, .что, если при скольжении по окружности тело фигуриста имеет общее вращение в сторону закривления дуги или в противоположную, это приведет к смещению мгновенной оси вращения, т. е. к искривлению дуги выезда из поворота внутрь или наружу.
Таким образом, практическая техника выполнения любых поворотов путем изменения момента инерции тела относительно продольной оси является неприемлемой для обязательных фигур.
Для того чтобы иметь правильное представление о механической сущности поворотов, целесообразно проанализировать движения на основе закона сохранения кинетического момента (см. раздел «Основы механики вращений»). В данном случае, говоря упрощенно, имеется в виду, что если на тело не действуют внешние силы, то вращение какого-либо звена в одном направлении вызывает поворот остальной части тела в противоположном. Количественно скорости этих встречных вращений обратно пропорциональны моментам инерции звеньев. Аналогичная зависимость существует и между углами поворота звеньев: поворот звена с малым моментом инерции (например, руки) на большой угол вызывает поворот на небольшой угол звена с большим моментом инерции (остальной части тела). Эту закономерность важно учитывать в технике поворотов.
Для упрощения картины исследуемого движения при предварительном рассмотрении пренебрежем внешними силами. Будем считать, что момент сил сопротивления, возникающий между коньком опорной ноги и льдом, равен нулю, т. е. силы сопротивления отсутствуют. На практике фигуристы высокого класса часто выполняют повороты так, что след, остающийся на льду, бывает исключительно тонким,—как говорят, волосяным. Совершенно очевидно, что в таких случаях величины моментов сил вращательного взаимодействия конька со льдом очень незначительны.
При начале разрешения поворота плечевой пояс выполняет так называемое обратное движение —плечевой пояс; и руки поворачиваются относительно таза. В силу закона сохранения кинетического момента это движение одновременно вызывает вращение нижней части тела в противоположном направлении. Важно отметить, что при правильном выполнении поворота во время обратного движения осуществляется и въезд в вершину элемента и выезд из него. В практике часто встречается ошибочное мнение о том, что обратному движению соответствует только выезд из вершины поворота. Итак, поворот верхней части тела в одном направлении вызывает поворот нижней части в другом. Тогда кинетический момент поворота верхней части тела должен быть равен кинетическому моменту нижней части тела: Kн = Kв Поскольку направления поворота верхней и нижней частей тела противоположны, получаем: 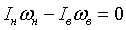 . Это значит, что вращение верхней части тела уравновешено вращением нижней его части таким образом, что общее вращение тела отсутствует и его суммарный кинетический момент равен нулю. Для получения более точной механической картины поворота несложно учесть влияние моментов сил сопротивления, возникающих между коньком и льдом. Очевидно, что моменты сил сопротивления направлены навстречу повороту конька, т. е. навстречу вращению нижней части тела. В результате силы сопротивления будут ослаблять вращение нижней части,—говоря иначе, уменьшать кинетический момент нижней части тела. При больших величинах сил сопротивления, возникающих между коньком и опорой, например при стоянии на резиновом коврике, поворот верхней части тела может не вызвать поворота нижней части с коньком. Условно обозначим потери кинетического момента в результате сил взаимодействия конька со льдом через Кв. Учитывая, что силы сопротивления направлены навстречу повороту нижней части тела с Коньками, можно написать: Кн-Кв-Кп = 0. . Это значит, что вращение верхней части тела уравновешено вращением нижней его части таким образом, что общее вращение тела отсутствует и его суммарный кинетический момент равен нулю. Для получения более точной механической картины поворота несложно учесть влияние моментов сил сопротивления, возникающих между коньком и льдом. Очевидно, что моменты сил сопротивления направлены навстречу повороту конька, т. е. навстречу вращению нижней части тела. В результате силы сопротивления будут ослаблять вращение нижней части,—говоря иначе, уменьшать кинетический момент нижней части тела. При больших величинах сил сопротивления, возникающих между коньком и опорой, например при стоянии на резиновом коврике, поворот верхней части тела может не вызвать поворота нижней части с коньком. Условно обозначим потери кинетического момента в результате сил взаимодействия конька со льдом через Кв. Учитывая, что силы сопротивления направлены навстречу повороту нижней части тела с Коньками, можно написать: Кн-Кв-Кп = 0.
Полученное соотношение является своего рода формулой поворота. Она позволяет проанализировать возможные искажения рисунка поворота в результате несбалансированного вращения нижней и верхней частей тела.
Случай 1. Кинетический момент нижней части тела больше суммы кинетического момента верхней части и кинетического момента потерь (Кн > Кв + Кп).
Практически это означает, что в результате разрешения вращение нижней части преобладает над противоположным ему вращением верхней части. В таком случае после поворота тело приобретает общее вращение в направлении, в котором вращалась опорная нога в повороте. Появление остаточного вращения тела в этом направлении вызывает характерный «перекрученный» рисунок поворота.
Случай 2. Кинетический момент нижней части тела меньше суммы кинетического момента верхней части и кинет-ческого момента потерь (Кн<Кв+Кп). В этом случае фигурист ощущает, что в результате разрешения обратное дви-жение, т. е. вращение плечевого пояса и рук, увлекло в поворот все тело. Это «останавливающее» вращение приводит к так называемой недокрученной форме поворота.
Искажение формы поворота тесно связано со смещением мгновенной оси вращения и обусловлено им. При вращении верхней части тела в сторону вращения нижней (Кн>Кв+Кп) мгновенная ось вращения смещается за пределы окружности и вызывает нарушение равновесия и соответствующее искажение следа. При Кн<Кв+Кп мгновенная ось вращения находится внутри круга и вызывает нарушение равновесия в ту же сторону и соответствующее искажение рисунка.
Итак, наличие общего вращения тела после поворота вызывает смещение мгновенной оси вращения, а в результате—нарушение равновесия и искажение рисунка поправи-лу, приведенному в начале раздела.
Поскольку при выполнении поворотов звенья тела фигуриста совершают вращательные движения, представляют интерес особенности геометрии отдельных фигур. Ведь при выполнении поворотов часть конька, соприкасающаяся со льдом, в точности повторяет контур фигуры.
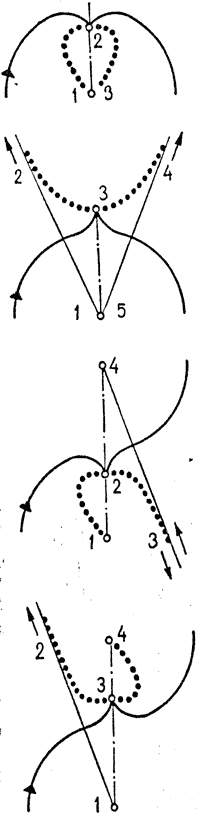 |
| Рис. 7. Центроиды движения конька в поворотах |
Одной из кинематических характеристик движения является так называемая центроида. Центроидой называют кривую, являющую собой геометрическое место точек мгновенных центров скоростей тела, т. е. точек, через которые проходят оси мгновенного вращения*. На рис. 7 приведены центроиды движения конька в поворотах тройкой, скобкой, крюком и выкрюком.
Несмотря на то что центроида — это кривая, по которой перемещается не реальное тело, а воображаемая точка, форма ее в определенной степени отражает геометрическую сложность траектории движения конька. Именно поэтому можно сделать предположение, что форма центроиды в каждом повороте отражает сложность выполнения элемента. Так, на рис. 7 видно, что в тройке центроида имеет форму плавной замкнутой кривой, расположенной внутри окружности. Она не имеет разрывов. Это говорит о том, что конек при скольжении не меняет направления вращения. В крюке ось мгновенного вращения конька последовательно проходит через точки 1, 2, 3, в точке 3 уходит в бесконеч» ность и затем переходит в точку 4— центр второго круга. В данном случае перемещение оси мгновенного вращения конька , более сложно.
* Мгновенной осью вращения называют ось, вокруг которой тело вращается в данный момент. Мгновенная ось вращения мо. жет не совпадать с продольной осью вращения тела.
Особую сложность имеет изменение направления врашения конька в конце выезда из поворота. Смена направления вращения конька в этой точке на практике часто сопровождается искажением следа. Наиболее распространенное из них — поздняя смена направления скольжения с характерной S-образной формой следа.
Аналогичная форма центроиды и в выкрюке. Разница лишь в том, что направление вращения конька меняется до поворота. Кривая центроиды в этой точке имеет разрыв, и именно в этом месте фигуры чаще встречаются искажения следа. Как правило, это S-образная форма подъезда к повороту.
Поскольку в выкрюке наиболее сложный участок (смена направления скольжения) расположен до поворота, а не после, как в крюке, фигурист проходит его почти в статическом, относительно более удобном положении. В результате устойчивость тела в выкрюке, как правило, лучше, чем в крюке, где направление скольжения меняется после поворота, на фоне сложного движения разрешения, после которого точность скольжения затруднена.
Наиболее сложная форма центроиды в повороте скобкой. Здесь она имеет два разрыва —до поворота и после него. Особенно трудно изменить направление скольжения конька после поворота, когда, как и в крюке, точность скольжения осложнена последствиями движения разрешения. Следует учитывать, что приведенные центроиды соответствуют движению конька, а не всего тела. Именно поэтому нельзя ставить знак равенства между вращениями конька и вращением всего тела.
Итак, можно сделать следующие выводы:
- При выполнении обязательных фигур телу фигуриста не должно сообщаться общее вращение вокруг его продольной оси.
- Механизм вращательного компонента поворотов заключается во встречном вращении верхней части тела относительно нижней. При этом кинетический момент нижней части тела равен по величине и противоположен по знаку кинетическому моменту верхней части тела и кинетическому моменту потерь.
- Показателем результирующего вращения частей тела является движение конька. Для точного соблюдения геометрической правильности кругов опорный конек фигуриста должен поворачиваться вокруг оси мгновенного вращения, проходящей через центр круга.
Форма поворотов может быть соблюдена, если при их выполнении опорный конек в каждый момент поворачивается вокруг оси мгновенного вращения, последовательно пере-мешающейся по эталонной центроиде поворота.
- Сложность выполнения поворота связана с конфигу-рацией центроиды движения конька в этом повороте.
Отталкивание
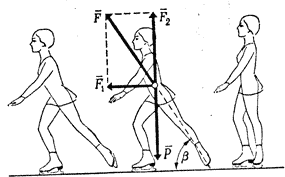
При выполнении больших фигур, таких, например, как параграф, фигурист совершает путь длиной около 170 м (9 кругов радиусом 3 м). На этом пути он делает 6 отталкиваний, после каждого отталкивания проезжая около 28 м. Естественно, что отталкивания, выполняемые для приобретения скорости, играют важную роль при выполнении фигуры. Фигурист получает начальную скорость, необходимую для выполнения обязательной фигуры, благодаря разгибанию толчковой ноги. Образующаяся при этом сила направлена вдоль прямой, соединяющей о.ц.т. тела с точкой касания конька толчковой ноги со льдом в конце отталкивания. Угол р, образованный силой отталкивания и ее проекцией на плоскость льда, назовем углом отталкивания.
На рис. 8 видно, что силу отталкивания F можно разложить на две составляющие:F1, и F2, из которых F2 уравновешивается силой веса Р, a F1 приводит фигуриста в движение. Таким образом, не вся сила отталкивания используется для сообщения фигуристу начальной скорости, а только одна из ее составляющих: F1. Обе они связаны соотношением F1 =FcosВ, где (В — угол отталкивания.
 |
| Рис. 8. Составляющие силы отталкивания |
Для определения величины силы отталкивания можно использовать извесщую в механике зависимость, которую для нашего случая можно записать в следующем виде: mV=F1t, где m—масса тела; V—скорость в конце отталкивания; F1 — горизонтальная составляющая силы отталкивания; t—время отталкивания.
В ряде случаев целесообразен короткий, энергичный толчок, в других — например, в петлях — незаметный, плавный не вызывающий изменения положения тела.
Дело в том что, приобретая нужную начальную скорость фигурист может варьировать силу отталкивания и его время в зависимости от двигательной задачи, т е. характера толчка.
Допустим, фигуристка весит 47,7 кг; для выполнения фигуры нужно иметь начальную скорость V = 2,4 м/с. Если отталкиваться в течение 0,3 с, необходима сила F1=(47,7*2,4)/(9,8*0.3).
— 39 кг, а если отталкивание продолжается 0,5 с, то для получения скорости V = 2.4 м/с достаточно силы 23,5 кг. Для данного веса фигуристки и заданной начальной скорости можно построить график изменения силы F в зависимости от времени отталкивания t (рис. 9).
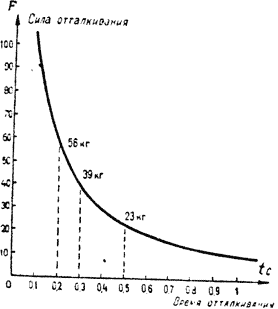 |
| Рис. 9 Связь силы отталкивания с временем отталкивания при определенном значении начальной скорости |
Время отталкивания в ряде случаев связано с конфигурацией толчковых следов. Так, одной из важных деталей техники отталкивания назад является длина толчковой дуги. Длинный толчковый «ус» часто встречается на практике и считается ошибкой. Для того чтобы овладеть техникой коротких толчков назад, необходимо правильно представлять направление действия сил реакции льда при отталкивании. На рис. 10 видно, что для выполнения короткого толчка усилие отталкивания по направлению совпадает или весьма близко к направлению предстоящего движения.
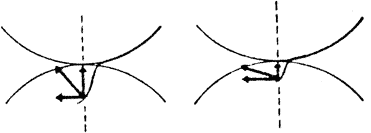 |
| Рис. 10. Направление сил реакции льда при выполнении коротких и длинных толчков |
В случае, если усилие отталкивания несколько запаздывает то сила отталкивания не совпадает с направлением предстоящего движения и «движущей» силой становится только составляющая силы отталкивания. В результате для придания телу достаточного количества движения необходимо увеличивать импульс силы, увеличивая время отталкивания. А это вызывает удлинение толчкового «уса». Таким образом, для выполнения короткого толчка необходимо, чтобы отталкивание выполнялось сразу же после того, как линия скольжения по кругу изогнулась. Эксперимент, проведенный автором с двумя кандидатами в мастера спорта, показал, что длина толчков назад в параграфах может быть уменьшена до размеров толчков вперед.
| 

Опорная нога— нога, на которой скользит фигурист
Свободная нога-нога, в данный момент не касающаяся льда. Смена направления — переход от скольжения вправо к скольжению влево или наоборот.
Смена фронта — изменение хода с переднего на задний или наоборот. Положение головы, свободной ноги и рук, спереди или сзади рассматривается по отношению к телу фигуриста, а не к направлению движения по льду (если это не оговаривается особо).
Скручивание туловища — поворот верхней части тела относительно нижней вокруг продольной оси.
Положительным направлением скручивания туловища считается направление в сторону закривления дуги.
Отрицательным направлением скручивания туловища считается направление, противоположное направлению закривления дуги.
Перевод - поворот плечевого пояса или головы вокруг продольной оси тела, а также связанное с этим изменение положения свободной ноги и рук.
Узел фигуры — часть рисунка, включающая толчки, начальные и конечные участки следов. Фигуры в форме кругов и восьмерок имеют один узел, фигуры в форме параграфа — два.